- 1. 過酷事故時原子炉建屋・格納容器の熱流動解析コード Advance/BAROC
- 1.1. 2. 特徴・機能
- 1.2. 3. 3次元圧縮性流体解析の基礎方程式
- 1.3. 4. 高速化・安定化のために採用した方法
- 1.4. 5. ECBA法
- 1.5. 6. 水蒸気凝縮モデル / 壁熱伝達モデル
- 1.6. 7. FPエアロゾル挙動解析モデル
- 1.7. 8. 解析事例
- 1.8. 8.1 過酷事故時原子炉建屋内水素分布解析
- 1.9. 8.2 過酷事故時原子炉建屋内水素・水蒸気分布解析
- 1.10. 8.3 過酷事故時原子炉建屋に移行するセシウム分布解析
- 1.11. 8.4 衝撃波管解析
- 1.12. 8.5 サーマルキャビティ解析
過酷事故時原子炉建屋・格納容器の熱流動解析コード Advance/BAROC
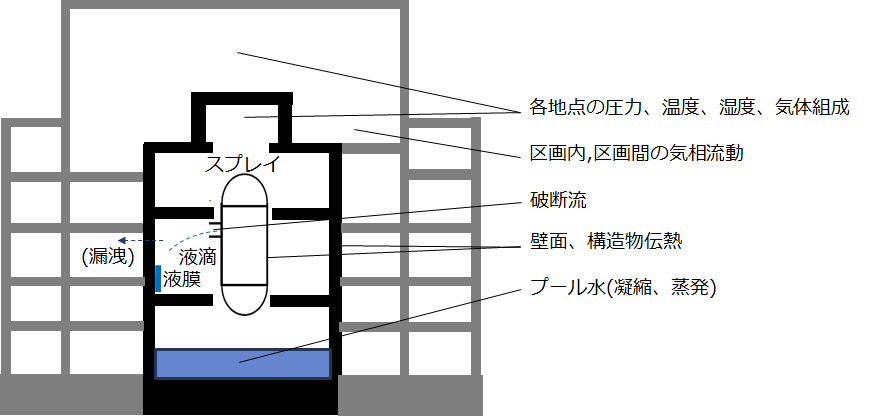
- 3次元熱流動解析は、原子炉格納容器および原子炉建屋の水素・水蒸気分布、セシウム挙動などを把握するうえで重要な解析項目
- そこで原子炉格納容器および原子炉建屋に特化した3次元圧縮性流体解析コードAdvance/BAROCを開発
- 物理法則に則って計算しつつ実用に耐えうる計算時間で現象を解析できるコードとして新たに開発
- 計算速度を重視し、高速化のために各種工夫を施した数値計算法を独自開発(ECBA法)
- Advance/BAROCコードでは計算体系の構築や物理現象モデルは原子炉格納容器および原子炉建屋に特化
2. 特徴・機能
- 多成分系の3次元圧縮性流体解析が可能
- 圧力・流速・エネルギーが強く結びついた陰解法 (ECBA法)や最新の行列計算法などにより高速で安定な流体計算
- Soave-Redlich-Kwong式、Peng-Robinson式などの状態方程式により実在流体物性を考慮
- NASA物性データベースより24種類の化学種の物性データを内蔵
- 乱流沈着、重力沈降、凝集(開発中)を考慮した放射性物質(FP)のエアロゾル挙動解析が可能
- k-εモデルによる乱流解析
- 水蒸気凝縮や壁熱伝達を考慮
| No. | 項 目 | 内 容 |
| 1 | 基礎方程式 | 多成分系ガスに対する3次元圧縮性流体に対する質量保存式、運動量保存式、エネルギー保存式および成分ガス濃度に対する質量保存式 |
| 2 | 状態方程式 | 完全理想気体、Soave-Redlich-Kwong式、Peng-Robinson式 NASA物性データベースより24種類の化学種の物性を用意 |
| 3 | 放射性物質(FP) | 液滴、固体粒子、エアロゾル粒子に対するパッシブスカラーの対流拡散を考慮した質量保存式 乱流沈着、重力沈降、凝集(開発中)を考慮 |
| 4 | 乱流モデル | k-εモデル |
| 5 | 水蒸気凝縮・熱伝達 | バルク凝縮、壁面凝縮、壁熱伝達 |
| 6 | 数値解法(陰解法) | 圧力・流速・エネルギーが強く結びついた解法 (ECBA法) SIMPLEC法 (MCBA法) |
| 7 | 行列計算法 | ILU(k)またはILUT/BiCGStab(l)法(行列反復解法ライブラリLis(注)を活用) |
| 8 | 計算格子 | 構造格子、スタッガード格子、マルチブロック (予定) |
| 9 | 対流項の差分法 | 一次精度風上差分法 2次・3次精度の制限関数minmod付きTVD法 |
(注) 日本発の行列反復解法ライブラリ Library of Iterative Solvers for linear systems, https://www.ssisc.org/lis/
3. 3次元圧縮性流体解析の基礎方程式
(1)質量保存式
(2) 運動量保存式
(3) エネルギー保存式
(4) 成分ガス濃度の質量保存式
4. 高速化・安定化のために採用した方法
(1)新たな陰解法として、圧力、流速、エネルギーが強く結びついたECBA法を開発
(2)圧力と流速の連成方法としてSIMPLEC法に基づく方法の採用
(3) 成分ガス濃度質量保存式の生成消滅項の線形化の工夫
凝縮や反応による物質の生成消滅項
をTaylor展開による線形化と、かつ、物質の質量分率がゼロ以下、1.0以上にならないようにすることにより比較的大きな時間スケールで安定的な計算が可能、次式右辺第1項をガス濃度質量保存式の左辺、次式第2項と第3項をガス濃度質量保存式の右辺に配置
(4) 最新の行列反復解法ライブラリLisの採用
5. ECBA法
(1) ECBA : Energy Conservation Based Algorithm
(2) 数値計算法の根幹である圧力Poisson方程式を、これまでのSIMPLE法系列の質量保存式ではなく、エネルギー保存式に基づいて組み立て圧力、流速、エネルギーが強く結びついた解法を独自に開発した。
(3) 変形したエネルギー保存式(赤く示した項を両辺に追加)
の左辺の全エネルギーEと運動量束ρuを次式に置き換えて離散化することで得られる圧力修正量
に関する圧力Poisson方程式の連立方程式を解く。
圧力Poisson方程式は次のように簡単に示すと、未知数である
に関する連立方程式としてまとめられる。右辺は荷重項として代数的に求める。
ECBA法はMCBA法(SIMPLEC法)と比べて、次のような特徴を持っている。
| No. | 項目 | ECBA法 | MCBA法(SIMPLEC法) |
| 1 | 質量の保存性 | 質量とエネルギーの保存式を適切に解くため、保証される。 | 圧縮性考慮のために保存式から得られた密度を状態方程式で得られる密度に置き換えるため、保証されない。 |
| 2 | 密度差が大きい流れ | 圧縮性を効果的に取り入れているため、密度差の大きい流れでも適切に計算できる。 | 圧縮性を効果的に入らないため、密度の大きい流体が密度の小さい流体に衝突した場合、密度の小さい流体が加速されすぎて不自然な流れになることがある。 |
| 3 | 熱的に大きな上昇を伴う流れ | 圧力、流速、エネルギーが強く結びついた解法のため、特別な処理なく適切に計算できる。 | 突発的に大きな熱発生があった場合、エネルギー変化に対して圧力や流速の変化が追い付けず、温度が異常になることがある。この場合、エンタルピーを状態方程式で得られるエンタルピーに置き換えることで改善することがある。 |
| 4 | 大きい乱流変動に誘起されるエネルギー・圧力変動 | 圧力、流速、エネルギーが強く結びついているため、流速変動è乱流変動è乱流拡散によるエネルギー変動è圧力変動è流速変動といった負のサイクルが生じて異常な熱流動変化になることがある。 | 圧力、流速とエネルギーの結びつきが弱く、左記の負のサイクルが生じにくい。 |
6. 水蒸気凝縮モデル / 壁熱伝達モデル
(1)バルク凝縮モデル
飽和水蒸気圧を越えた量を凝縮緩和時間で凝縮させるモデル
凝縮時は潜熱を考慮するものの、凝縮した水蒸気の質量、エネルギーは計算体系から削除
(2) 壁面凝縮モデル
液膜を仮定し気体と液膜との熱伝達、液膜と壁面との熱伝達および凝縮に伴う熱伝達の熱収支に基づくモデル
(3) 壁熱伝達モデル
厚みを考慮した壁の内外の熱伝達と壁の熱伝導による熱収支に基づくモデル
7. FPエアロゾル挙動解析モデル
(1) 基礎方程式
エアロゾル濃度をパッシブスカラー(トレーサー)とした対流拡散方程式
(2) 拡散・慣性衝突による乱流沈着速度[1]
(3) 重力沈降速度
(4) 凝集による生成消滅
乱流運動衝突、浮力・重力衝突、層流剪断衝突による凝集[2]
8. 解析事例
- 8.1 過酷事故時原子炉建屋内水素解析
- 8.2 過酷事故時原子炉建屋内水素・水蒸気分布解析
- 8.3 過酷事故時原子炉建屋に移行するセシウム分布解析
- 8.4 衝撃波管解析
- 8.5 サーマルキャビティ解析
8.1 過酷事故時原子炉建屋内水素分布解析
(1)原子炉建屋に対して、0.5m～0.6mで格子分割し実時間24時間の解析
(2)主要な計算条件は次のとおり
①計算格子数：633,600
②酸素、窒素、水素、水蒸気の4成分
③流入条件：5階シールドプラグより計算開始から4.4時間一定流入。水素134kg/210kg/400kg 流入温度1,000K
④壁熱伝達を考慮
⑤実在流体の状態方程式(Soave-Redlich-Kwong式)を使用
⑥時間刻み幅は最大Courant数1,000として制御
(3)24時間の解析に要した計算時間(単CPU計算※)
①水素134kg：8 hr 25 min 28 s
②水素210kg：8 hr 57 min 9 s
③水素400kg：9 hr 48 min 22 s
※使用した計算機スペック
機種名：PowerEdge R640 / CPU：Intel Gold 5218 @ 2.30GHz / メモリー：96GB / OS ：CentOS Linux release 7.6.1810
水素流入開始時の水素濃度分布変化(水素210kg)
水素流入後30分から6時間までの流速分布変化(水素210kg)
水素流入後30分から6時間までの水素濃度分布変化(水素210kg)
(1)機器ハッチ側から見たモデル図
(2)(1)とは逆側から見たモデル図
8.2 過酷事故時原子炉建屋内水素・水蒸気分布解析
(1)原子炉建屋に対して、0.5m～0.6mで格子分割し実時間24時間の解析
(2)主要な計算条件は次のとおり
①計算格子数：633,600
②酸素、窒素、水素、水蒸気の4成分
③流入条件：5階シールドプラグより計算開始から4.4時間一定流入。水蒸気5,250kg＋水素134kg/210kg/400kg 流入温度1,000K
④水蒸気凝縮、壁熱伝達を考慮
⑤実在流体の状態方程式(Soave-Redlich-Kwong式)を使用
⑥時間刻み幅は最大Courant数1,000として制御
(3)24時間の解析に要した計算時間(単CPU計算※)
①水素134kg：11 hr 13 min 14 s
②水素210kg：12 hr 56 min 12 s
③水素400kg：12 hr 36 min 19 s
※使用した計算機スペック
機種名：PowerEdge R640 / CPU：Intel Gold 5218 @ 2.30GHz / メモリー：96GB / OS ：CentOS Linux release 7.6.1810
水素流入後24時間までの水素濃度分布変化(水素210kg)
(1)機器ハッチ側から見たモデル図
(2)(1)とは逆側から見たモデル図
水素・水蒸気・空気の三元図[4]での位置づけ
[4]Z.M. Shapiro, T.R. Moffette, HYDROGEN FLAMMABILITY DATA AND APPLICATION TO PWR LOSS-OF-COOLANT ACCIDENT, WAPD-SC-545, U.S. Atomic Energy Commission, Pittsburgh, PA, 1957, 13 pp
8.3 過酷事故時原子炉建屋に移行するセシウム分布解析
(1)原子炉建屋に対して、0.3m～1.0mで格子分割し実時間24時間の解析
(2)主要な計算条件は次のとおり
①計算格子数：270,864
②酸素、窒素、水素、水蒸気の4成分
③FPエアロゾル：CsOH(粒子密度3,680kg/m3) 粒径は1μm と 10μm の2種類
④流入条件：原子炉ウェルトップフランジにおいて計算開始から4.4時間一定流入。
水蒸気5,250kg＋水素210kg
FPエアロゾル：0.01kg/s(1μm)、0.01kg/s(10μm)
⑤水蒸気凝縮、壁熱伝達を考慮
⑥実在流体の状態方程式(Soave-Redlich-Kwong式)を使用
⑦時間刻み幅は最大Courant数2,000として制御
(3)24時間の解析に要した計算時間(単CPU計算※)
13 hr 30 min 4 s
※使用した計算機スペック
機種名：PowerEdge R640 / CPU：Intel Gold 5218 @ 2.30GHz / メモリー：96GB / OS ：CentOS Linux release 7.6.1810
流入後24時間の流速分布変化
(1)ケース1
(2)ケース2
流入中は、ケース1のほうがシールドプラグ漏洩口からの流速が大きい。
流入停止後も、ケース1のほうがオペレーションフロアでの流速が大きい。
流入後24時間のセシウムエアロゾル濃度分布変化
(1)ケース1
(2)ケース2
①ケース1でのシールドプラグへの沈着量が最も多い
②シールドプラグ底面への沈着量はケース2のほうが多い
③オペフロ天井や壁への沈着量はケース1のほうが多い
④天井のシールドプラグ中央直上は沈着量が少ない
⑤天井や壁の隅に比較的多く沈着する傾向
粒径別セシウム沈着量分布
セシウム沈着量変化の比較
8.4 衝撃波管解析
- 圧縮性流体解析の標準問題
- 高圧部と低圧部の流体が仕切板によって分けられた管路において、仕切り板を瞬時に取り除いたときの圧力等の変化を厳密解[1]と比較
- 計算条件
i.ケース1
高圧部 : 圧力 1.0MPa、温度 350K
低圧部 : 圧力 0.1MPa、温度 280K
X=0.5m 、格子分割数 : 200、1,000,000
完全理想気体、比熱比 1.4
ii.ケース2
高圧部 : 圧力 1.0MPa、温度 800K
低圧部 : 圧力 0.1MPa、温度 300K
X=0.1m 、格子分割数 : 200 完全理想気体、比熱比 1.4
[1] Sod, G. A., "A Survey of Several Finite Difference Methods for Systems of Nonlinear Hyperbolic Conservation Laws”, J. Comput. Phys. 27 (1978) 1–3.
8.5 サーマルキャビティ解析
- 自然対流解析、熱伝導解析の標準問題
- 加熱面と冷却面に挟まった正方形内の自然対流解析
- 最も著名なベンチマーク解[2]と比較
- 計算は次のケースを実施
加熱面 : 温度 280K
冷却面 : 温度 270K
X=1.0m 、格子分割数 : 100×100
完全理想気体、比熱比 1.4
Prandtl数 0.71、Rayleigh数 1,000
重力加速度 9.80665[m/s2]
[2]de Vahl Davis, G., “Natural convection of air in a square cavity: A benchmark numerical solution”, Int. J. Numer. Methods Fluids, 3 (1983) 249-254.
| No. | 項目 | 本計算[注1] | ベンチマーク解[注2] | 備考 |
| 1 | 平均Nusselt数 | 1.140(+1.97%) | 1.118 | 加熱面と冷却面の温度差で無次元化した温度勾配を加熱面に沿って積分 |
| 2 | 水平方向最大流速 | 3.608(-1.12%) | 3.649 | 最大流速は高さと温度拡散係数(熱伝導度と熱容量の比)で流速を無次元化 |
| 3 | 垂直方向最大流速 | 3.683(-0.38%) | 3.697 | 最大流速は高さと温度拡散係数(熱伝導度と熱容量の比)で流速を無次元化 |
[注1]カッコ内の数値はベンチマーク解との差異
[注2]de Vahl Davis, G., “Natural convection of air in a square cavity: A benchmark numerical solution”, Int. J. Numer. Methods Fluids, 3 (1983) 249-254.
エネルギー保存式とガス濃度質量保存式に対して同一条件とした解析
Ra=1,000となるように、密度、粘性係数、熱伝導度、拡散係数を与える。
加熱面：温度1.0K、質量分率：1.0
冷却面：温度0.0K、質量分率：0.0
分子量がほぼ等しい2成分の解析
窒素と一酸化炭素の2成分、Ra=1,000となるように輸送係数を1,000倍とした
加熱面：温度280.0K、質量分率：窒素0.0、一酸化炭素1.0
冷却面：温度270.0K、質量分率：窒素1.0、一酸化炭素0.0
